# 数据结构
理论和实践相结合,总是最佳的学习途径,推荐刷leetcode来巩固和加深数据结构。实践案例可查看个人leetcode (opens new window),提供算法总结、题解分析以及详细注释。
# 1. 线性表:数组、链表、栈、队列
线性表是为了解决单线存储而出现的。最基础结构为数组和链表,栈和堆是线性表的特殊形态,在操作上进行了限制。构造一个栈或堆结构,既可以使用数组,也可以使用链表。
# 1.1 数组
数组:就是最简单粗暴的存储方法。就是直接拉出一大块数据存在那里。数组的快速存取其实只是一个副作用,因为所有的数据都在一起,可以直接算出来数据的地址。数组的优势是连续内存,可以快速读取。缺点是插入比较困难,需要后面数据挪位置。
c/c++语言的数组更接近数据结构的数组概念,默认是不能动态扩容的。js高级语言的数组概念就包含更多,比如动态扩容、语言层自实现栈、队列特性。
# 1.2 链表
链表:则是为了解决可以无线增长的需求。因为找不到一大块可以连续的存入数据,甚至也不知道程序可能使用的数据总量,所以就没办法划分一块数据来使用,划小了不够用,划大了浪费(这在早年是非常大的事情)。所以必须想办法解决问题。最后采用的方法就是从入口开始,每一个数据块不仅仅有数据,还会有指向下一个数据块的线索,用来寻找下一个数据。这就是链表。
// js链表数据结构
let Node = function(element) {
this.element = element
this.next = null // 下个node的引用(在js语言中,Node类已经是引用类型了)
}
所谓的双向链表,只是加了一个向前的线索的链表而已。不仅如此,队列,栈,都是线性表的特殊形态。进行了操作上的限制罢了。既可以是数组,也可以是链表。
// js双向链表数据结构
let Node = function(element) {
this.element = element
this.next = null
this.prev = null
}
数组和链表都是一种数据结构,数组是开辟整块内存,链表则拥有next指针,指向下一个node节点。
# 1.3 堆、栈/队列
都是一种数据结构。
- 堆:堆是一种
经过排序的树形数据结构,每个结点都有一个值。通常我们所说的堆的数据结构,是指二叉堆。堆的特点是根结点的值最小(或最大),且根结点的两个子树也是一个堆(有序)。由于堆的这个特性,常用来实现优先队列。堆的存取是随意,这就如同我们在图书馆的书架上取书,虽然书的摆放是有顺序的,但是我们想取任意一本时不必像栈一样,先取出前面所有的书,书架这种机制不同于箱子,我们可以直接取出我们想要的书。 - 栈:属于一维线性关系,加上
后进先出规则。后存放的先取,先存放的后取,无法从中间插入和删除。 - 队列:也属于一纬关系,
先进先出规则。
千万不要把堆和队列搞混了,它们是三种不同的数据结构,栈和队列相似,堆完全不同。
# 1.3.1 堆和栈的应用
- 栈:最常见的应用就是
执行栈,当有大函数嵌套小函数时,先逐一把所有函数压入栈中。依据后进先出,先执行最后的小函数,直到执行完所有函数。 - 堆:在js等高级语言中,基本类型有Undefined、Null、Boolean、Number 和String。这些类型在内存中分别占有固定大小的空间,所以使用栈空间来保存。而
引用类型,你根本不知道这个类型要用多大的内存空间,所以使用堆存储最好不过。
# 1.3.2 为什么会有栈内存和堆内存之分
通常与垃圾回收机制有关。为了使程序运行时占用的内存最小。
当一个方法执行时,每个方法都会建立自己的内存栈,在这个方法内定义的变量将会逐个放入这块栈内存里,随着方法的执行结束,这个方法的内存栈也将自然销毁了。因此,所有在方法中定义的变量都是放在栈内存中的;
当我们在程序中创建一个对象时,这个对象将被保存到运行时数据区中,以便反复利用(因为对象的创建成本通常较大),这个运行时数据区就是堆内存。堆内存中的对象不会随方法的结束而销毁,即使方法结束后,这个对象还可能被另一个引用变量所引用(方法的参数传递时很常见),则这个对象依然不会被销毁,只有当一个对象没有任何引用变量引用它时,系统的垃圾回收机制才会在核实的时候回收它。
在c语言这类没有垃圾回收机制的语言中,定义基本类型如char时,系统会自动在栈上为其开辟空间,而堆是需要程序员自己申请空间,如malloc(10)。由于栈上的空间是自动分配自动回收的,所以栈上的数据的生存周期只是在函数的运行过程中,运行后就释放掉,不可以再访问。而堆上的数据只要程序员不释放空间,就一直可以访问到,不过缺点是一旦忘记释放会造成内存泄露。
# 1.4 总结
- 数组(连续存储);
- 链表(离散存储);
- 有序表:要求插入元素时,对元素对值进行比较,以找到相应的插入位置。
- 顺序表、单链表、循环链表、双向链表
- 栈(线性结构常见应用,由链表或数组增删和改进功能实现),特点是先进后出;
- 队列(线性结构常见应用,由链表或数组增删和改进功能实现),特点是先进先出;
数组和链表是最基础的数据结构,相同的功能实现可以用数组结构,也可以用链表结构,如栈与队列的实现,可以底层存储是用数组,也可以是小块内存链接起来的链表。再比如数组的reverse翻转,使用数组或链表数据结构,相关算法是完全不一样的。
# 2. 集合、字典/散列表
都属于非顺序数据结构。
集合:一组无序且唯一的项组成,可以理解为没有重复元素且没有顺序的数组(集合只存储value)。Javascript ES6新增Set数据结构即为此。- js set原生方法:set.values()/set.has(value)/set.add(value)/set.delete(value)
字典:也称作映射,使用{key:value}键值对的形式存储数据。Javascript ES6新增Map数据结构即为此。- js map原生方法:map.keys()/map.values()/map.has(key)/map.set(key,value)/map.delete(key)
- 散列表:是实现字典的一种方式,散列算法的作用,是尽可能在数据结构中找到一个值(O(1)时间复杂度)。其中最重要的,就是选择好一个
散列函数,给定一个键值,然后返回值在表中的位置。
# 3. 树
树是为了解决单一入口下的非线性关联性的数据存储或者排序这样的功能而来的。
二叉树:二叉树的节点最多只能有两个节点(左、右节点)二叉搜索树:二叉树的一种,左节点比父节点小,右节点比父节点大。自平衡树- 自平衡二叉搜索树(AVL):任何一个节点左右两侧子树的高度差最多为1.
B树、B+树红黑树
最常见的应用是编程时候的map,就是利用了二叉树的可排序和可以快速插入并且保持序列完整的特性来构建键值数据对,来实现数据的插入增加以及快速查找的能力的。
还有做语法解析,文字处理等等很多场景也会用到树。这就不一一赘述了。当然在吃透线性表的基础上,再去理解树也并不难。因为在本质上,树相对于链表,就是每个节点不止有一个后续节点但是只有一个前置节点。
没有环的链表,也可看作一颗树
# 4. 算法
通过算法来学习数据结构很有效。
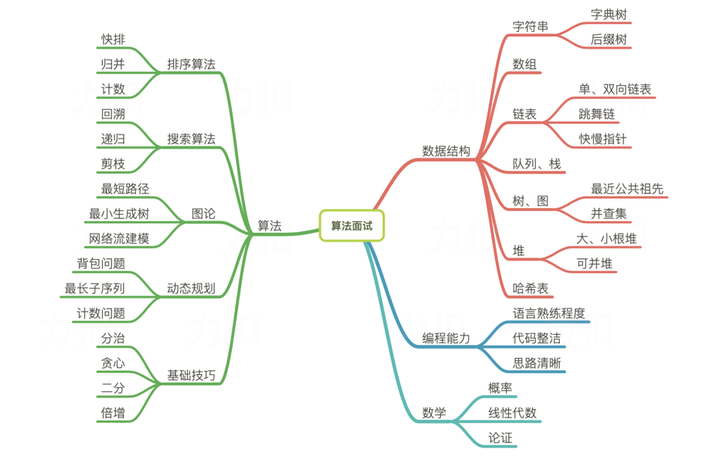
# 4.1 算法思想
# 1. 分治法(递归是分治的常用算法)
将原问题分解为若干个规模较小但类似于原问题的子问题(Divide),「递归」的求解这些子问题(Conquer),然后再合并这些子问题的解来建立原问题的解。
# 2. 动态规划
动态规划其实和分治策略是类似的,也是将一个原问题分解为若干个规模较小的子问题,递归的求解这些子问题,然后合并子问题的解得到原问题的解。
区别在于这些子问题会有重叠,一个子问题在求解后,可能会再次求解,于是我们想到将这些子问题的解存储起来,当下次再次求解这个子问题时,直接拿过来就是。
其实就是说,动态规划所解决的问题是分治策略所解决问题的一个子集,只是这个子集更适合用动态规划来解决从而得到更小的运行时间。
即用动态规划能解决的问题分治策略肯定能解决,只是运行时间长了。因此,分治策略一般用来解决子问题相互对立的问题,称为标准分治,而动态规划用来解决子问题重叠的问题。
# 3. 其他
- 贪心算法: 算法简单,运算非常快。可能不能获得最优解,但非常接近
- 回溯法
# 4.2 常见算法
- 排序
- 冒泡排序
快速排序
- 搜索
二分法:针对有序数组双指针法二叉搜索树:针对排好序的二叉树。递归
深度优先搜索(DFS):优先深度,一条道走到黑。根据打印前后又分:前序、中序(中序遍历二叉查找树可得到一个关键字的有序序列)、后序递归DFS:递归处理left节点,然后递归right节点即可栈数据结构的DFS(空间换时间):递归处理left,right节点使用栈(后进先出)保存起来,当left处理完再pop出栈顶元素作为当前node。
广度优先搜索(BFS): 按照树的depth,依次搜索递归BFS: 先递归获得depth值,再foreach lever递归搜索队列数据结构的BFS: 使用队列,依次放入当前队列第一位的left、right节点,同时pop当前队列第一位,进行删除。
# 4.3 常见大O运行时间:
- O(log n),也叫对数时间,如:二分查找
- O(n), 线性时间,如:简单查找
- O(nlog n) 如:快速排序
- O(n2) 如:冒泡算法、选择排序算法,属于较慢的一种算饭
- O(n!) 非常慢的算法
对数概念:log10100等同于“将多少个10相乘的结果为100”,所以log10100=2(2个10相乘等于100)。对数运算是幂运算的逆运算,使用大O表示法时,log指的是log2,所以一般二分法是logn。
O(log n)比O(n)快,当搜索的元素越多时,前者比后者快的越多。
# 二分法
二分查找要求线性表具有有随机访问的特点(例如数组),也要求线性表能够根据中间元素的特点推测它两侧元素的性质,以达到缩减问题规模的效果。
针对有序数组,每次排除一半的选项,算法复杂度:O(logn)。
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
// https://leetcode-cn.com/problems/binary-search
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var search = function(nums, target) {
// 二分法,二分下标
var left = 0, right = nums.length - 1
while(left <= right) {
let mid = left + Math.floor((right - left) / 2)
if (nums[mid] === target) return mid
if (nums[mid] > target) right = mid - 1 // 最大值为mid-1
else left = mid + 1 // 最小值为mid + 1
}
return -1
};
# 快速排序
常用来数组排序,以某个数为基准,大于放置在数右边,小于则放置在左边。O(nlogn)
// js语言快速排序
// js语言特性中,数组取用/连接较为方便,原生提供,所以直接取中间值比较
function quickSort(arr) {
if (arr.length <= 1) return arr
let left = []
let right = []
let middleIndex = Math.floor(arr.length / 2)
let middle = arr.splice(middleIndex, 1)
arr.forEach(item => middle > item ? left.push(item) : right.push(item))
return quickSort(left).concat(middle).concat(quickSort(right))
}
quickSort([12,2,3, 23,8])